Stats 13

Lecture 2

Introduction to data
reporting & visualization

Guillaume Calmettes

Last time

Importance of visualization to better understand data
=> e.g. Soho epidemics map

Why visualize your data?

Anscombe's quartet

	Dataset #1		Dataset #2		Dataset #3		Dataset #4
	x	y	x	y	x	y	x	y
	10	8.04	10	9.14	10	7.46	8	6.58
	8	6.95	8	8.14	8	6.77	8	5.76
	13	7.58	13	8.74	13	12.74	8	7.71
	9	8.81	9	8.77	9	7.11	8	8.84
	11	8.33	11	9.26	11	7.81	8	8.47
	14	9.96	14	8.1	14	8.84	8	7.04
	6	7.24	6	6.13	6	6.08	8	5.25
	4	4.26	4	3.1	4	5.39	19	12.5
	12	10.84	12	9.13	12	8.15	8	5.56
	7	4.82	7	7.26	7	6.42	8	7.91
	5	5.68	5	4.74	5	5.73	8	6.89
Regression

	Dataset #1		Dataset #2		Dataset #3		Dataset #4
Mean	9	7.5	9	7.5	9	7.5	9	7.5
Variance	11	4.1	11	4.1	11	4.1	11	4.1
Correlation	0.86		0.86		0.86		0.86
Regression line	y = 3 + 0.5x		y = 3 + 0.5x		y = 3 + 0.5x		y = 3 + 0.5x

Why visualize your data?

Describing a dataset

When describing a dataset, we generally consider the following three questions:

What is the general shape of the data?
Where are the data values centered?
How do the data vary?

These are all aspects of what we call the distribution of the data.

-- 1 --
Shape

General shape of a distribution

A symmetric distribution is one in which the left and right hand sides of the distribution are roughly equally balanced.
A skewed (non-symmetric) distribution is a distribution in which there is no such equal balance. Right-skewness refers to a longer right tail, while left-skewness correspond to a longer left tail.
A uniform distribution is a specific symmetric distribution in which all outcomes are equally likely.

Data distribution examples

Internet access in the world

Time between eruptions of the Old Faithful geyser (1978-1979)
- Yellowstone National Park -

Proportions for categorical variables

Proportions are also called relative frequencies and we can display them in a relative frequency table.

Is there one true love
for each person?
(Phone survey, 2010)

Response	Frequency	Relative Frequency
Agree	735	0.28
Disagree	1812	0.69
Don't know	78	0.03
Total	2625	1.00

Notation for a proportion:
The proportion for a population is denoted $\pi$
The proportion for a sample is denoted $\overset{\hat{}}{p}$ (read “p-hat”)

Distribution of proportion data

Note:
Lengths are easier to visually compare than area

Distribution of proportion data

Stacked bars (overall quantity)

Layered bars (distribution of values in the categories)

Grouped bars (comparison of categories + items)

Distribution of quantitative variables

A common way to visualize the shape of a moderately sized dataset is a dotplot.

Species	Longevity	Species	Longevity	Species	Longevity	Species	Longevity	Species	Longevity
Baboon	20	Chimpanzee	20	Fox	7	Leopard	12	Rabbit	5
Black bear	18	Chipmunk	6	Giraffe	10	Lion	15	Rhinoceros	15
Grizzly bear	25	Cow	15	Goat	8	Monkey	15	Sea lion	12
Polar bear	20	Deer	8	Gorilla	20	Moose	12	Sheep	12
Beaver	5	Dog	12	Guinea Pig	4	Mouse	3	Squirrel	10
Buffalo	15	Donkey	12	Hippopotamus	25	Opossum	1	Tiger	16
Camel	12	Elephant	40	Horse	20	Pig	10	Wolf	5
Cat	12	Elk	15	Kangaroo	7	Puma	12	Zebra	15

Note:
For this particular dataset, values are integers and can be easily stacked.

Simplifying a dotplot

A dotplot can be hard to build, and dots can overlap (visually) if the values are very similar and a lot of values are represented.

1- Define "boundaries"

2- Count the number of elements inside each zone

This is the process to make what is called a histogram.

The histogram

Dataset:

36	25	38	46	55	68	72	55	36	38
67	45	22	48	91	46	52	61	58	55

Bin	Frequency	"Scores" included
20-30	2	25, 22
30-40	4	36, 38, 36, 38
40-50	4	46, 45, 48, 46
50-60	5	55, 55, 52, 58, 55
60-70	3	68, 67, 61
70-80	1	72
80-90	0	--
90-100	1	91

Note:
- Number of bins = $\sqrt{n}$ is a good start to explore your data.
- Usually all the bins cover the same data range (similar bin width), but uneven bins can also be constructed.

A histogram is a plot that lets you discover, and show, the underlying frequency distribution (shape) of a set of continuous data. This allows the inspection of the data for its underlying distribution (e.g., normal distribution), outliers, skewness, etc.
To construct a histogram from a continuous variable you first need to split the data into intervals, called bins.
Notice that, unlike a bar chart, there are no "gaps" between the bars (although some bars might be "absent" reflecting no frequencies). This is because a histogram represents a continuous data set, and as such, there are no gaps in the data (although you will have to decide whether you round up or round down scores on the boundaries of bins).
There is no right or wrong answer as to how wide a bin should be, but there are rules of thumb. You need to make sure that the bins are not too small or too large.
=> We can see from the histogram on the left that the bin width is too small because it shows too much individual data and does not allow the underlying pattern (frequency distribution) of the data to be easily seen. At the other end of the scale is the diagram on the right, where the bins are too large, and again, we are unable to find the underlying trend in the data.
Histograms are based on area, not height of bars! In a histogram, it is the area of the bar that indicates the frequency of occurrences for each bin. This means that the height of the bar does not necessarily indicate how many occurrences of scores there were within each individual bin. It is the product of height multiplied by the width of the bin that indicates the frequency of occurrences within that bin. One of the reasons that the height of the bars is often incorrectly assessed as indicating frequency and not the area of the bar is due to the fact that a lot of histograms often have equally spaced bars (bins), and under these circumstances, the height of the bin does reflect the frequency.
The major difference is that a histogram is only used to plot the frequency of score occurrences in a continuous data set that has been divided into classes, called bins. Bar charts, on the other hand, can be used for a great deal of other types of variables including ordinal and nominal data sets.

The characteristics of a histogram

Distribution:

Normalize bar height

Bins #:

Sort dataset

-- 2 --
Central tendency

The mean

A common measure of central location is the (arithmetic) mean. It is sometimes called the average.

$\bar{x}=\sum x_{i}$

$\bar{x}$ for a sample (read "x-bar")
$\mu$ for a population

Which corresponds to:

$\bar{x}=\frac{x_{1}+x_{2}+...+x_{n}}{n}$

$\bar{x}=\frac{\textrm{sum of all the observations}}{\textrm{number of observations}}$

The trimmed mean

A trimmed mean refers to the calculation of the mean after discarding given parts of a sample (or distribution) at the high and low end (typically discarding an equal amount of both).

Some people consider that the use of a trimmed mean "helps" eliminate the influence of data points on the tails that may affect the traditional mean.

$\bar{x}=\frac{1+23+19+24+17+26+20+23+89+82}{10}=32.4$

$\bar{x}_{trimmed}=\frac{23+19+24+17+26+20+23}{7}=21.7$

Never use it!

The median

The median of a set of ordered data values is:
- the middle entry (for an odd number of entries)
- the average of the middle 2 values (for an even number
of entries)

mean of $(\frac{n}{2})^{th}$ and $(\frac{n}{2}+1)^{th}$ observations

$(\frac{n+1}{2})^{th}$ observation

The mode

The mode is the value that occurs most often in the dataset. If no value in the dataset is repeated, then there is no mode this particular dataset.

What is the mode in the dataset below?

Multimodal distribution

In a bimodal distribution, the taller peak is called the major mode and the shorter one is the minor mode.

Resistance

The term resistance is related to the impact of outliers on a statistic. In general, we say that a statistic is resistant if it is relatively unaffected by extreme values.

The median and the mode are resistant, while the mean is not.

2.5

3.2

3.5

3.9

4.0

4.4

5.3

5.9

6.1

6.4

Mean: 4.52
Median: 4.2

Mean: 6.84
Median: 4.4

Averages can be misleading

Pick your central descriptor wisely

Number of children per household in China (2012)

Mean: 1.55
Median: 1

More representative of the "typical" 2012 family
(One Child Policy)

Other locations

The minimum is the smallest number in the (sorted) dataset.

The maximum is the largest number in the (sorted) dataset

-- 3 --
Variation, spread

The standard deviation

A common measure of data variability is
the standard deviation (SD). It measures the spread of the data in a sample

$s=\sqrt{\fragindex{0}{\fraglight{highlight-red-gc}{\frac{\sum(x_{i}-\bar{x})^2}{n-1}}}}$

Variance

$s$ for a sample
$\sigma$ for a population

$s=\sqrt{\frac{(x_{1}-\bar{x})^2+(x_{2}-\bar{x})^2+...+(x_{n}-\bar{x})^2}{n-1}}$

$s=\sqrt{\frac{\textrm{sum of observed squared difference from sample mean}}{\textrm{number of observations - 1}}}$

The SD can be loosely interpreted as the typical distance (in absolute value) between the data values and the mean of the distribution.

The larger the standard deviation, the more variability there is in the data and the more spread out the data are.

In practice, we generally compute the standard deviation using a calculator or computer software. The units for the standard deviation are the same as the units for the original data.

We would want the average of the sample variances for all possible samples to equal the population variance. It seems like a logical property and a reasonable thing to happen. This is called “unbiased” When we divide by (n −1) when calculating the sample variance, then it turns out that the average of the sample variances for all possible samples is equal the population variance. So the sample variance is what we call an unbiased estimate of the population variance. If instead we were to divide by n (rather than n −1) when calculating the sample variance, then the average for all possible samples would NOT equal the population variance. Dividing by n does not give an “unbiased” estimate of the population standard deviation. Dividing by n−1 satisfies this property of being “unbiased”, but dividing by n does not. Therefore we prefer to divide by n-1 when calculating the sample variance.

The standard deviation

Let's consider 2 sets of data, both have a mean of 100

Numbers	Mean	SD
100, 100, 100, 100, 100	100	0
90, 90, 100, 110, 110	100	10

Set 1: all values are equal to the mean, so there is no variablility at all

Set 2: one value equals the mean and other four values are 10 points away from the mean. So the average distance away from the mean is about 10

Example for Set 2:

Calculate the sample mean: $\bar{x}=100$
For each observation, calculate the difference between the data value
and the mean: [-10, -10, 0, 10, 10]
Square each difference in step 2: [100, 100, 0, 100, 100]
Sum the squared differences in step 3, and then divide this sum by $(n-1)$:
variance $s^2=\frac{400}{5-1}=\frac{400}{4}=100$
Take the square root of the value in step 4: $s=\sqrt{100}=10$

Beware of the standard deviation

Like the mean, the standard deviation does not cope well with skewed distributions.

The SD is only useful in the context of the normal distribution

The Empirical Rule: For any bell-shaped curve, approximately
- 68% of the values fall within 1 SD of the mean in either direction
- 95% of the values fall within 2 SD of the mean in either direction
- 99.7% of the values fall within 3 SD of the mean in either direction

Misuse of SD is everywhere

The range

The range gives you the most basic information about the spread of a dataset. It is calculated by the (arithmetic) difference between the lowest and highest data value.

Interquantile range

The median divides the data into two equal halves (it is the $50^{th}$ percentile). If we divide each of those halves again, we obtain two additional statistics known as the first (Q1) and third (Q3) quartiles, which are the $25^{th}$ and $75^{th}$ percentiles.

Interquartile range: $\textrm{IQR} = Q3 − Q1$

A value is considered an outlier if it is:

smaller than $Q1−1.5\times IQR$
larger than $Q3+1.5\times IQR$

Percentiles

The $k^{th}$ percentile is a value in the dataset that has $k\%$ of the data values at or below it and $(100 – k)\%$ of the data values at or above it.

Note:
Here our dataset contains 40 data points. So each data point correspond to $\frac{100}{40}=2.5\%$ of the data.

Present your
(quantitative) data

Bar graphs are evil

1) Part of the range covered by the bar might have never been observed in the sample

Bar graphs are evil

2) They conceal the variance and the underlying distribution of the data

Look the same?

It's not!

Bar graphs are evil

3) They are associated with (usually not defined) error bars

Different types, different meanings:
- Descriptive statistics (SD, range)
- Inferential statistics (SEM, CI)

Avoid making bar graphs

To reveal the distribution of the data:

Display data in their raw form
A dot plot is a good start
Dynamite plunger plots conceal data
Check the pattern of distribution of the values

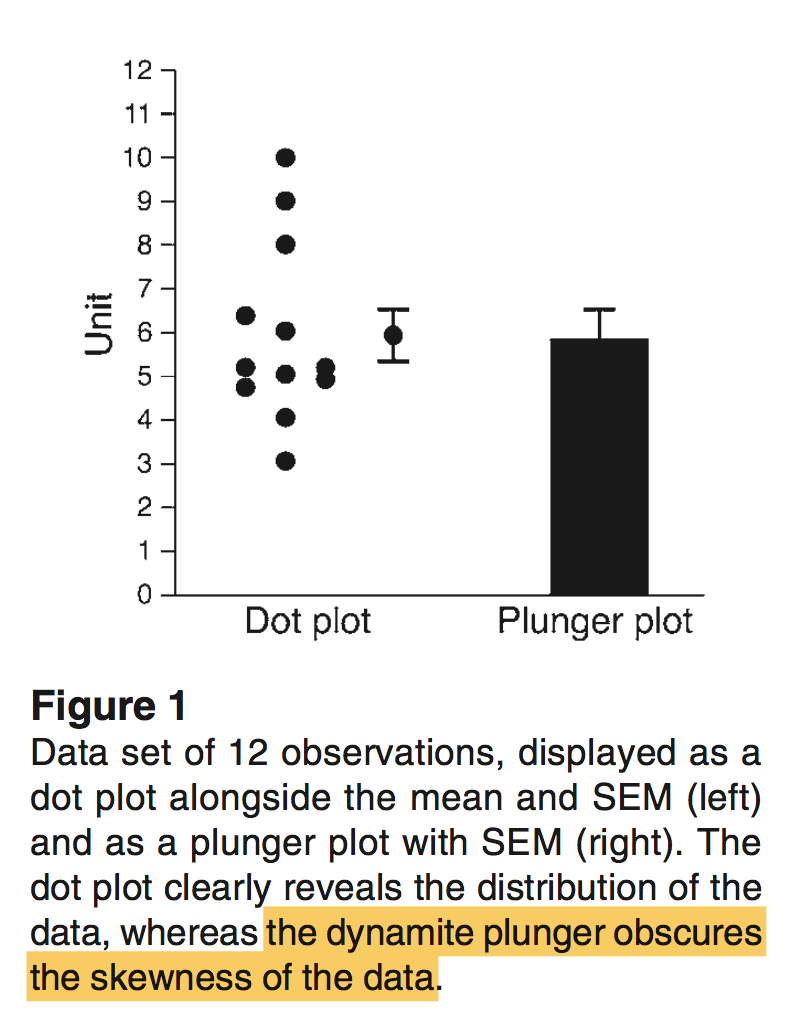
About Figure 1:

First set: Gaussian (or normal) distribution (symmetrically distributed)
Second set: right skewed, lognormal (few large values). This type of distribution of values is quite common in biology (ex: plasma concentrations of immune or inflammatory mediators)”

Plunger plots only: who would know that the values were skewed [...] and that the common statistical tests would be inappropriate?”

"For better characterization of a sample, we prefer dots plots, or box plots for their ability to display a minimum of five measures of the underlying data."

Avoid making bar graphs

Impact Factor: 12.575 (2015).
The JCI is one of the top journals in the “Medicine, Research & Experimental” category.

To maintain the highest level of trustworthiness of data, we are encouraging authors to display data in their raw form and not in a fashion that conceals their variance.

Presenting data as columns with error bars (dynamite plunger plots) conceals data. We recommend that individual data be presented as dot plots shown next to the average for the group with appropriate error bars (Figure 1).

Avoid making bar graphs

[...] the amount of information they provide is still limited to two values, the mean and the spread.

"For better characterization of a sample, we prefer dots plots, or box plots for their ability to display a minimum of five measures of the underlying data."

You've been warned before!

Dotplot

If the number of data is relatively small, showing directly the raw data and accompanying mean/median is best.

Boxplot

A boxplot is a graphical display of the five number summary for a quantitative variable. It shows the general shape of the distribution, identifies the middle 50% of the data, and highlights any outliers.

A boxplot includes:

A box stretching from Q1 to Q3
A line that divides the box drawn at the median
A line from each quartile to the most extreme data value that is not an outlier. (if no outliers minimum and maxixum)
Each outlier plotted individually

Boxplot (example)

The gallery of
bad data reporting

Common mistakes in data reporting

Relative frequencies MUST sum up to 1 (100%)

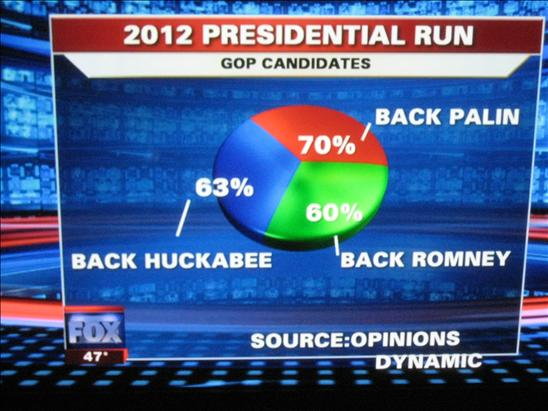
Common mistakes in data reporting

Relative frequencies MUST sum up to 1 (100%)

Data in pie-chart are hard to interpret

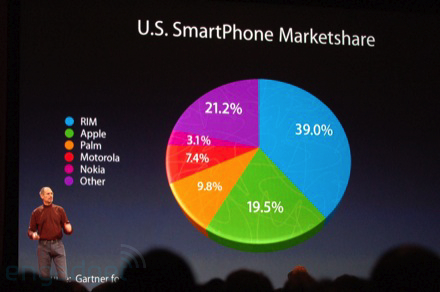
Common mistakes in data reporting

Relative frequencies MUST sum up to 1 (100%)

Data in pie-chart are hard to interpret

3D graphs are misleading

Common mistakes in data reporting

Relative frequencies MUST sum up to 1 (100%)

Data in pie-chart are hard to interpret

3D graphs are misleading

Zero your scale

Common mistakes in data reporting

Relative frequencies MUST sum up to 1 (100%)

Data in pie-chart are hard to interpret

3D graphs are misleading

Zero your scale

Common mistakes in data reporting

Relative frequencies MUST sum up to 1 (100%)

Data in pie-chart are hard to interpret

3D graphs are misleading

Zero your scale

Labels MUST correspond to data

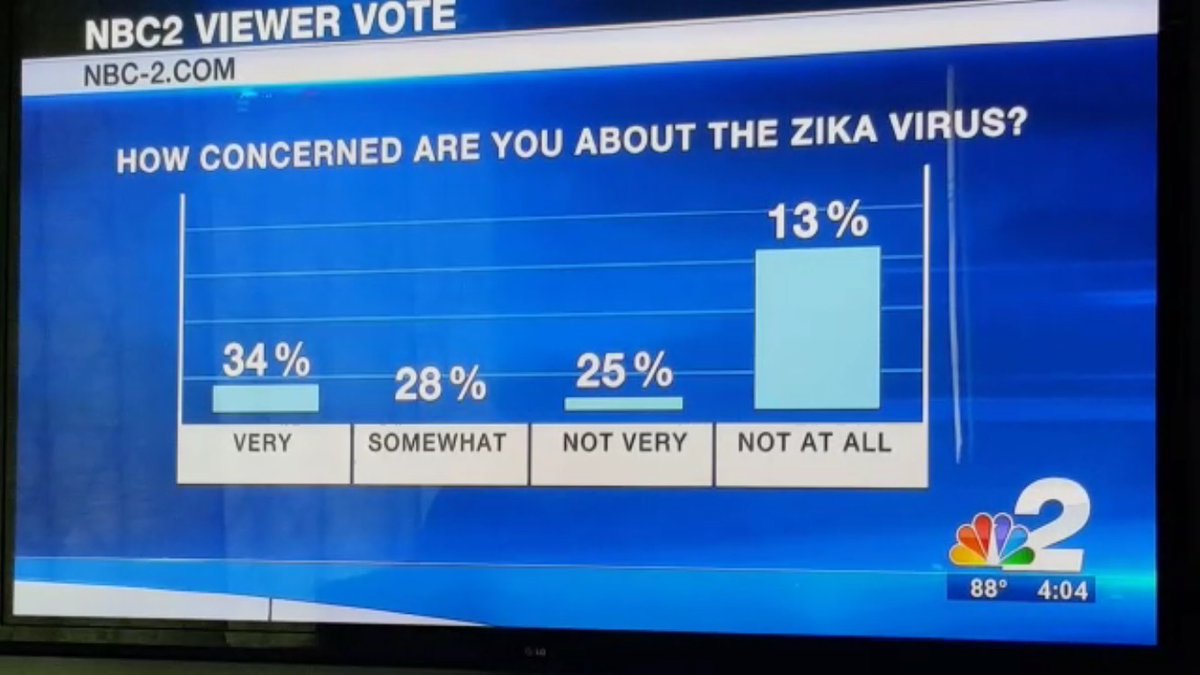
Common mistakes in data reporting

Relative frequencies MUST sum up to 1 (100%)

Data in pie-chart are hard to interpret

3D graphs are misleading

Zero your scale

Labels MUST correspond to data

Stats 13

Lecture 2

Introduction to data reporting & visualization

Last time

Why visualize your data?

Why visualize your data?

Describing a dataset

-- 1 -- Shape

General shape of a distribution

Data distribution examples

Proportions for categorical variables

Distribution of proportion data

Distribution of proportion data

Distribution of quantitative variables

Simplifying a dotplot

The histogram

The characteristics of a histogram

-- 2 --Central tendency

The mean

The trimmed mean

The median

The mode

Multimodal distribution

Resistance

Averages can be misleading

Pick your central descriptor wisely

Other locations

-- 3 --Variation, spread

The standard deviation

The standard deviation

Beware of the standard deviation

The SD is only useful in the context of the normal distribution

Misuse of SD is everywhere

The range

Interquantile range

Percentiles

Present your (quantitative) data

Bar graphs are evil

Bar graphs are evil

Bar graphs are evil

Avoid making bar graphs

Avoid making bar graphs

Avoid making bar graphs

You've been warned before!

Dotplot

Boxplot

Boxplot (example)

The gallery of bad data reporting

Common mistakes in data reporting

Common mistakes in data reporting

Common mistakes in data reporting

Common mistakes in data reporting

Common mistakes in data reporting

Common mistakes in data reporting

Common mistakes in data reporting

Introduction to data
reporting & visualization

-- 1 --
Shape

-- 2 --
Central tendency

-- 3 --
Variation, spread

Present your
(quantitative) data

The gallery of
bad data reporting